 |
|
Рассмотрим два случая
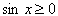 и и
 |
 |
|
Если
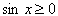 , то , то
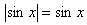 и исходное уравнение равносильно каждому из уравнений и исходное уравнение равносильно каждому из уравнений
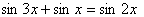 , ,
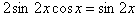 , ,
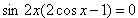 (1). (1).
Уравнение (1) равносильно совокупности уравнений: |
 |
|
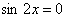 (2)
(2) |
 |
|
 (3)
(3) |
 |
|
Условию
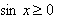 удовлетворяет следующие две серии корней уравнения (2): удовлетворяет следующие две серии корней уравнения (2):
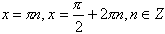 . . |
 |
|
А также корни уравнения (3) такие, что
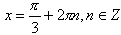 . . |
 |
|
Если
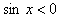 , то , то
 и исходное уравнение равносильно каждому из уравнений и исходное уравнение равносильно каждому из уравнений
 , ,
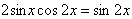 , ,
 (4).
(4).
Уравнение (4) равносильно совокупности уравнений: |
 |
|
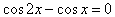 |
 |
|
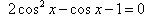 . .
Откуда получаем
 (и тогда (и тогда
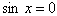 ) и ) и
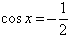 (5). (5). |
 |
|
Таким образом, если
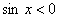 , то все корни исходного уравнения содержатся среди корней уравнения (5), т.е. среди чисел вида , то все корни исходного уравнения содержатся среди корней уравнения (5), т.е. среди чисел вида

|
 |
|
Ответ
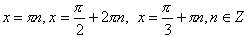 |
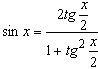 ,
,
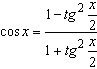 .
. .
.